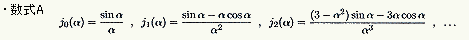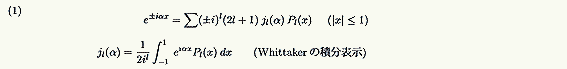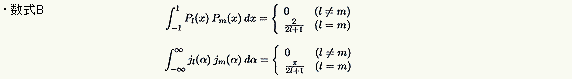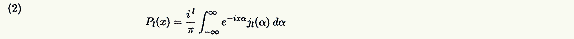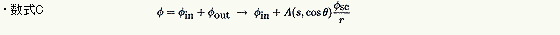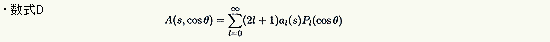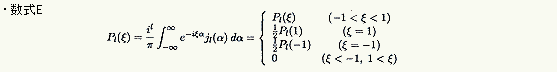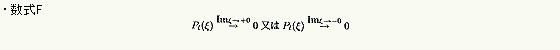■ 古いがあまり知られていないお話
ルジャンドルの多項式Pι(x) と球ベッセル関数jι(α) のフーリエ変換関係
三上 浩佳 （文理10回卒／群馬県桐生市在住） 11AUG.2010
 今回のお話は、見たところページの空白が数式で埋められ無味乾燥なものに見えて興味をそがれる方も多いでしょうが、「こんなこともあるんだ」というような軽い気持ちで読み流していただければ幸いです。
＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊ ＊
さて、標題を目にして、物理数学の達人の諸兄には「そんなことあるの？」といぶかる方も多いと思います。今もどこの大学でも話題にのぼることはないでしょうし、和洋を問わずどの数学公式集にも載っていないのですから無理からぬことです。
学生時代を振り返って物理数学の公式集をパラパラとめくってみたとしましょう。ルジャンドルの多項式Pι(x) は量子力学に良く出てきました。球ベッセル関数jι(α)については、情報理論や通信工学など振動系をやった人は目に
したことがあるかもしれません。ベッセル関数というのは聞いたことがあるが、
球ベッセル関数というの何だろうという人も多いでしょう。
球ベッセル関数というのは、通常のベッセル関数のオーダーが半整数のものを言い、次のような三角関数の集まりからなる関数群です。
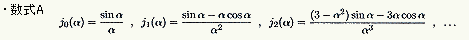
ここからは、岩波書店版数学公式集３の表記に準じて表すことにします。基本的には、x もαも複素数で良いのですが、とりあえず実数ということにしておきましょう。
ところで、ルジャンドルの多項式Pι(x)と球ベッセル関数jι(α)の２つの関数はまるで兄弟のような振る舞いをもっているようなのです。たとえば、この稿に関連するものを挙げると
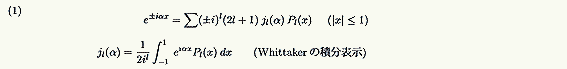
があります。さらに、２つの関数は共通の直交関係という性質をもっております。
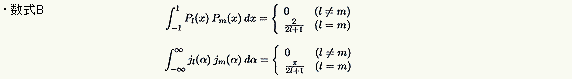
これらの式をうまく使うと、
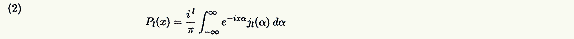
という式が導けます(註＊1)。この公式は、(1) 式のちょうど逆の関係になっていますが、不思議なことにどの公式集にも載っていません。どうやら誰も気付いていなかったということらしいのです。
どうしてWhittaker の積分表示の逆の表現にこだわったかというと、次のような事情があります。
量子力学で粒子間の衝突を扱うとき、衝突系全体の波動関数Φを入射波Φin と透過波Φout の２つの部分に分けて表現します。透過波Φoutは粒子間の相互作用によって散乱中心からいろいろな方向に散らばって行きますから、この透過波が散乱波Φsc と呼ばれるものになります。このとき、散乱波を表す波
動関数の前にどんな方向に多く散乱されるかの確率を表す係数を付けて、相互
作用の性質を表す因子とするのです。この因子を散乱振幅と言います。つまり、
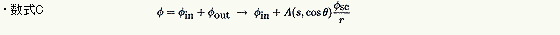
と表したときのA(s,cosθ) が散乱振幅です。s は系の全エネルギー、θは散乱角です。r は散乱中心からの距離ですが、全く均等に粒子が散乱される場合は球面波を形成するはずですから、あらかじめ係数の中に組み込んでおくと
いう訳です。
具体的には、散乱振幅の絶対値の２乗｜A(s,cosθ)｜2 が散乱の方向分布(微分断面積) に結びつき、散乱振幅の虚部ImA(s,cosθ) が散乱の全断面積、
つまり散乱の起こる確率の大小に直結します。
さらに、散乱振幅A(s,cos θ) をとびとびの軌道角運動量量子数l に対応する部分波に分けて、
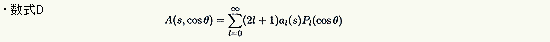
と表すことがあります。aι(s) は部分波振幅と呼ばれるものです。見てのとおり、散乱振幅が和の形で表されていますが、これは非常に不便です。
この和を積分の形で表現するために昔から多くの人がいろいろな工夫をしたのですが、なかなかうまい表現法を見つけることができませんでした。上の(2) 式も純粋の数学公式から導かれた訳けではなく、散乱振幅の式をいろいろ
いじくっているうちに半ば偶然に発見されたものなのです。
ですから、(2) 式を検証するには、力ずくでやるよりも、(2) 式を仮定して球ベッセル関数の直交関係を用い、それがルジャンドルの多項式Pι(x) になるというのが手っ取り早い方法です。
上の(1) 式と(2) 式を見比べてみると、(1) 式の積分領域を除けば互いがフーリエ変換の関係に似た形をもっていますから、フーリエ変換の関係を導けそうな気がしてきます。本当にそうなのでしょうか。
これが調べられたのはかなり後のことです。Pι(x) とjι(α) の変数を複素数に拡張し、さらに球ハンケル関数と呼ばれる関数を導入し、複素平面内に上半分と下半分の無限大の半円の周りに一周線績分をします。このとき球ハンケル関数の原点における特異点が重要な役割を果たしています。
ここで、フーリエ変換の形を想定したのですから、x = -1 とx = 1（ここからは変数を複素数ξに変えますので、x はξの実部ということになります）のところで不連続になることに留意しなければなりません。つまり、線績分を３つの場合に分けて実行するのです。そんなこんだで、
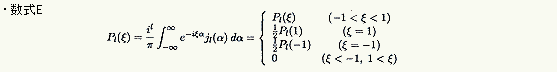
という結果に到達します(※)。詳細は省きますが、興味のある方は引用文献(註＊2) を参照して下さい。
さて、Pι(x) とjι(α) とがフーリエ変換の関係にあることが粒子間の衝突問題にどんな有り難みを生み出すのでしょうか。散乱振幅を和の形から積分の形に置き換えることができることばかりではありません。一般のフーリエ変換の性質をフルに使うことができます。
フーリエ変換を得意としている方はいろいろな活用法を思い浮かべるかもしれません。近くは、医療画像（超音波診断、ＣＴ、ＭＲI など）の作像アルゴリズムにも採用されております。粒子衝突系の散乱現象では、例えば情報理論や通信工学で良く用いられる伝達関数と応答関数の関係を応用するというのも
一つの考えかもしれません(註＊2)。でも、これ以上は話が長くなりますし、この
稿の目的を越えてしまいます。何より退屈するでしょうね。応用のお話は皆さ
んのアイデアにお任せするとして、今回のお話はこの辺で失礼させていただき
ましょう。
※最後の式の（ ξ < -1,1 < ξ ）のところは、
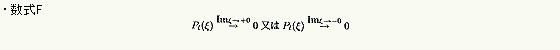
またPι(1)及びPι(-1) は、おのおのPι( ξ → +1) 及びPι( ξ → -1) という意味です。
■ 引用文献
(註＊1) H. Mikami, Lett. Nuovo Cimento 10(1974) 661
(註＊2) Hiroyoshi MIKAMI, Prog.Theor.Physics 87(1992) 991
|
